3 Generalized Linear Models

3.1 Components of a Generalized Linear Model

3.1.1 Random Component

3.1.2 Linear Predictor

\[\alpha + \beta_1x_1+ ... + \beta_px_p.\]

3.1.4 Ordinary Linear Model: GLM with Normal Random Component

3.2 Components of a Generalized Linear Model

3.2.1 Linear Probability Model

\[ P(Y=1) = \alpha + \beta_1x_1 + ... + \beta_px_p.\]

3.2.2 Logistic Regression Model

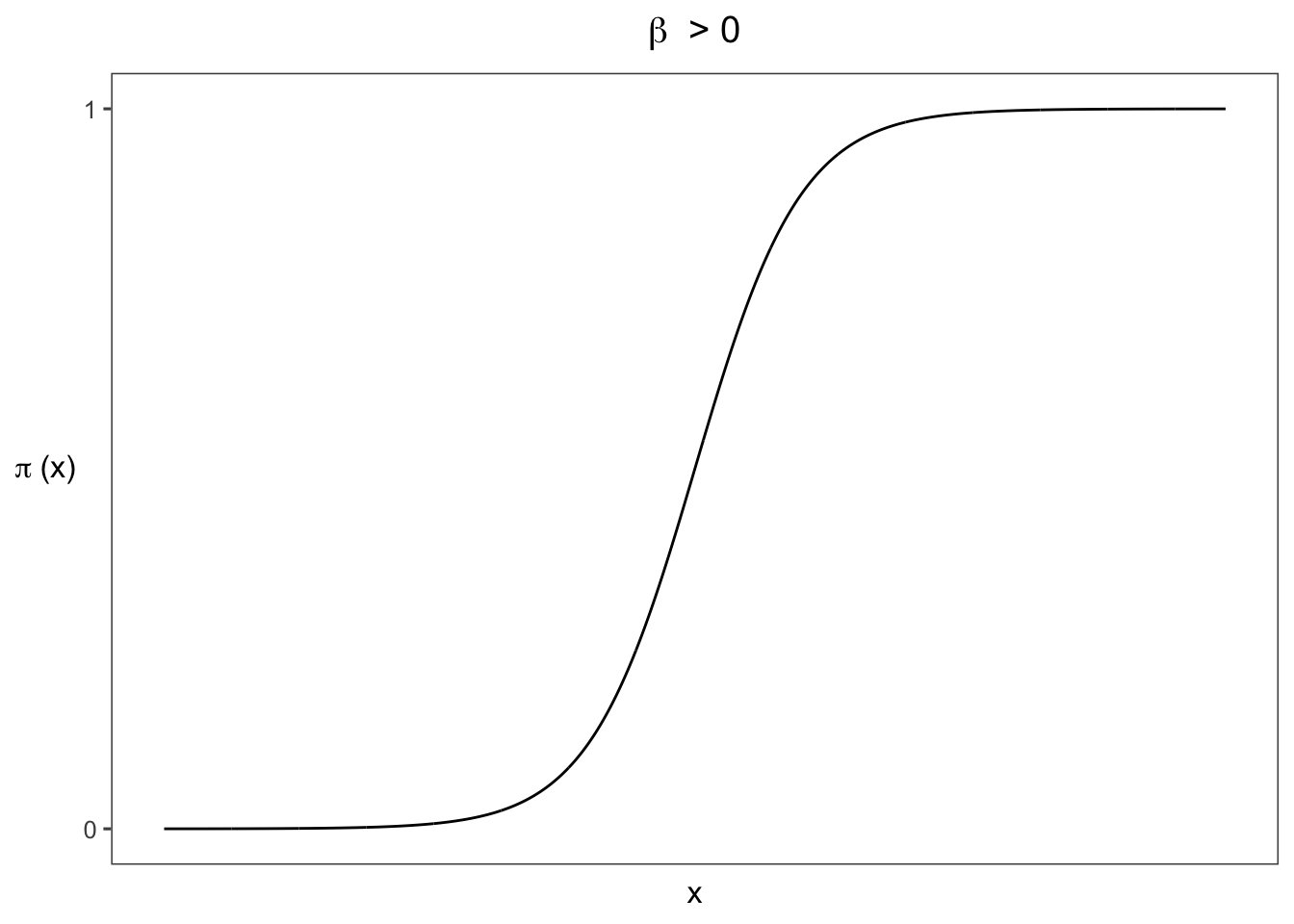
\[\begin{equation} P(Y=1) = \frac{exp(\alpha + \beta x)}{exp(1+\alpha + \beta x}=\frac{e^{\alpha + \beta x}}{1 + e^{\alpha + \beta x}}, \tag{3} \end{equation}\]

\[\mathrm{log}\left[\frac{P(Y=1)}{1-P(Y=1)}\right] = \alpha + \beta_1x_1 + ... + \beta_px_p.\]

3.2.3 Example Snoring and Heart Disease

snore <- matrix(c(24, 1355, 35, 603, 21, 192, 30, 224), ncol = 2, byrow = TRUE)

`Table 3.1` <-  
  bind_cols(Snoring = c("Never", "Occasionaly", "Nearly every night", 
                        "Every night"),
            as.data.frame(snore)) %>% 
  rename("Yes" = V1, "No" = V2) %>% 
  mutate(Proportion = round(Yes / (Yes + No), 3)) %>% 
  bind_cols(`Linear Fit` = c(0.017, 0.057,0.096,0.116),
            `Logistic Fit` = c(0.021, 0.044,0.093,0.132))
  

knitr::kable(`Table 3.1`)
Snoring Yes No Proportion Linear Fit Logistic Fit
Never 24 1355 0.017 0.017 0.021
Occasionaly 35 603 0.055 0.057 0.044
Nearly every night 21 192 0.099 0.096 0.093
Every night 30 224 0.118 0.116 0.132

3.2.4 Using R to Fit Generalized Lineare Models for Binary Data

Heart <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Heart.dat", 
                       header = TRUE, stringsAsFactors = FALSE)
knitr::kable(Heart)
snoring yes no
never 24 1355
occasional 35 603
nearly_every_night 21 192
every_night 30 224 
library(tidyverse)
Heart <- Heart %>% 
  mutate(snoringNights = recode(snoring, never = 0, occasional = 2, 
                                nearly_every_night = 4, every_night = 5)) 

n <- Heart$yes + Heart$no

fit <- glm(yes/n ~ snoringNights, family = binomial(link = logit), 
           weights = n, data = Heart)

summary(fit)

Call:
glm(formula = yes/n ~ snoringNights, family = binomial(link = logit), 
    data = Heart, weights = n)

Deviance Residuals: 
      1        2        3        4  
-0.8346   1.2521   0.2758  -0.6845  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -3.86625    0.16621 -23.261  < 2e-16 ***
snoringNights  0.39734    0.05001   7.945 1.94e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 65.9045  on 3  degrees of freedom
Residual deviance:  2.8089  on 2  degrees of freedom
AIC: 27.061

Number of Fisher Scoring iterations: 4
fitted(fit)
         1          2          3          4 
0.02050742 0.04429511 0.09305411 0.13243885 
fit2 <-  glm(yes/n ~ snoringNights, 
             family = quasi(link = identity, variance = "mu(1-mu)"), 
             weights = n, data = Heart)
summary(fit2)

Call:
glm(formula = yes/n ~ snoringNights, family = quasi(link = identity, 
    variance = "mu(1-mu)"), data = Heart, weights = n)

Deviance Residuals: 
       1         2         3         4  
 0.04478  -0.21322   0.11010   0.09798  

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.0172467  0.0006402   26.94 0.001375 ** 
snoringNights 0.0197778  0.0005204   38.01 0.000692 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for quasi family taken to be 0.03441852)

    Null deviance: 65.904481  on 3  degrees of freedom
Residual deviance:  0.069191  on 2  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 3

3.2.5 Data Files: Ungrouped or Grouped Binary Data

Heart2 <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Heart2.dat", 
                       header = TRUE, stringsAsFactors = FALSE) %>% 
    mutate(snoringNights = recode(snoring, never = 0, occas = 2,
                                  nearly = 4, every = 5)) 

Heart2 %>% 
  filter(row_number() %in% c(1, 2, n())) 
  subject snoring x y snoringNights
1       1   never 0 1             0
2       2   never 0 1             0
3    2484   every 5 0             5
fit <- glm(y ~ snoringNights, family = binomial(link = logit), 
           data = Heart2)

summary(fit)

Call:
glm(formula = y ~ snoringNights, family = binomial(link = logit), 
    data = Heart2)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-0.5331  -0.3010  -0.2036  -0.2036   2.7882  

Coefficients:
              Estimate Std. Error z value Pr(>|z|)    
(Intercept)   -3.86625    0.16621 -23.261  < 2e-16 ***
snoringNights  0.39734    0.05001   7.945 1.94e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 900.83  on 2483  degrees of freedom
Residual deviance: 837.73  on 2482  degrees of freedom
AIC: 841.73

Number of Fisher Scoring iterations: 6

3.3 Generalized Linear Models for Binary Data

3.3.1 Poisson Distribution for Counts

\[E(Y) = \mathrm{var}(Y)= \mu,\ \ \ \sigma(Y)=\sqrt{\mu}.\]

3.3.2 Poisson Loglinear Model

\[\mathrm{log}\ \mu = \alpha + \beta x.\] \[\begin{equation} \mu = \mathrm{exp}(\alpha+\beta x) = e^\alpha(e^\beta)^x. \tag{4} \end{equation}\]

3.3.3 Example: Female Horseshoe Crabs and their Satellites

Crabs <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Crabs.dat", 
                       header = TRUE, stringsAsFactors = FALSE) %>% 
  tibble() %>% 
  select(color, spine, width, weight, sat)  
  
Crabs %>% 
  rename("C" = color, "S"=spine, "Wi"=width, "Wt"=weight, "Sa"=sat) %>% 
  slice_head(n=6) %>% 
  knitr::kable()
C S Wi Wt Sa
2 3 28.3 3.05 8
3 3 22.5 1.55 0
1 1 26.0 2.30 9
3 3 24.8 2.10 0
3 3 26.0 2.60 4
2 3 23.8 2.10 0 
fit <- glm(sat ~ width, family = poisson(link=log), data = Crabs)
summary(fit)

Call:
glm(formula = sat ~ width, family = poisson(link = log), data = Crabs)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.8526  -1.9884  -0.4933   1.0970   4.9221  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.30476    0.54224  -6.095  1.1e-09 ***
width        0.16405    0.01997   8.216  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 632.79  on 172  degrees of freedom
Residual deviance: 567.88  on 171  degrees of freedom
AIC: 927.18

Number of Fisher Scoring iterations: 6
suppressPackageStartupMessages(library(gam))

suppressWarnings(
  gam.fit <- gam(sat ~ s(width), family = poisson, data = Crabs)
)

plot(sat ~ width, xlab = "Width", ylab = "Number of satelites", data = Crabs)
curve(predict(gam.fit, data.frame(width = x), type = "resp"), add = TRUE)

Crabs$gamPrediction <- predict(gam.fit, type = "resp")

# https://stackoverflow.com/questions/2631780/r-ggplot2-can-i-set-the-plot-title-to-wrap-around-and-shrink-the-text-to-fit-t
wrapper <- function(x, ...) {paste(strwrap(x, ...), collapse = "\n")}

library(ggthemes)


Crabs %>% 
  ggplot(aes(x = width, y = sat)) +
  geom_point(shape = 1, size = 3) +
  geom_line(aes(y=gamPrediction)) +
  xlim(c(20, 35))+
  theme_few() + 
  xlab("Width") +
  ylab("Number of satelites") +
  ggtitle(wrapper("Figure 3.3.  Number of satellites by female crab shell width (in centimeters), and generalized additive model smoothing fit.", 70))

\[\hat\mu =\mathrm{exp}(\hat\alpha + \hat\beta x)= \mathrm{exp}[-3.305 + 0.164(26.3)]=2.74.\]

identityGLM <-  glm(sat ~ width, 
                    family = poisson(link="identity"), 
                    start=c(0.5,0.5),
                    data = Crabs)

logitGLM <- glm(sat ~ width, family = poisson(link="log"), data = Crabs)

Crabs2 <- bind_cols(Crabs, 
                    "identity" = fitted(identityGLM),
                    "logit" = fitted(logitGLM))
       
library(RColorBrewer)
colors <- brewer.pal(n = 4, name = "Dark2")

CrabBin <- Crabs2 %>% 
  mutate(bin = case_when(width <= 23.25 ~ 23, 
                         width > 23.25 & width <= 24.25 ~ 24, 
                         width > 24.25 & width <= 25.25 ~ 25, 
                         width > 25.25 & width <= 26.25 ~ 26, 
                         width > 26.25 & width <= 27.25 ~ 27, 
                         width > 27.25 & width <= 28.25 ~ 28, 
                         width > 28.25 & width <= 29.25 ~ 29, 
                         width > 29.25 ~ 30)) %>% 
  group_by(bin) %>% 
  summarize(Mean = mean(sat, na.rm=TRUE), .groups = "drop") 

  library(ggthemes)

  ggplot() + 
  geom_point(data = CrabBin, aes(x=bin, y = Mean)) +
  geom_line(data = Crabs2, aes(x=width, y = identity, color = colors[1])) +
  geom_line(data = Crabs2, aes(x=width, y = logit, color = colors[2]))  +
  coord_cartesian(ylim = c(0, 5.5), xlim = c(22, 32)) +
  scale_y_continuous(breaks=seq(0, 5)) +
  scale_x_continuous(breaks=seq(22, 32, by = 2)) +
  theme_few() +
  annotate(geom = "segment", x = 23, y = 2.1, xend = 23, yend = 1.67, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[1]) +
  annotate(geom = "text", x = 22.5, y = 2.25, label = "Log link", 
           hjust = "left", color = colors[1]) +
  annotate(geom = "segment", x = 24.5, y = 1.6, xend = 24, yend = 1.6, 
           arrow = arrow(length = unit(2, "mm")), color = colors[2]) +
  annotate(geom = "text", x = 24.6, y = 1.6, label = "Identity link", 
           hjust = "left", color = colors[2]) +
  theme(legend.position = "none") +
  xlab("Width") +
  ylab("Mean Number of Satellites")

3.3.4 Overdispersion: Greater Variability than Expected

3.4 Generalized Lineaer Models for Counts and Rates

3.4.1 Wald, Likelihood-Ratio, and Score Inference Use the Likelihood Function

\[z = \hat\beta /SE,\]

\[2\ \mathrm{log}(\ell_1/\ell_0) = 2[\mathrm{log}(\ell_1) - \mathrm{log}(\ell_0)] = 2(L_1-L_0),\].

# https://stackoverflow.com/questions/29642867/drawing-a-tangent-to-the-plot-and-finding-the-x-intercept-using-r

x = seq(-3.0, 7, by = .01)

df <- tibble(x = x) %>% 
  mutate(y = 10 - (x-2)^2 )

  
spl <- smooth.spline(df$x, df$y, spar=0.3)
newx <- seq(min(df$x), max(df$x), 0.1)
pred <- predict(spl, x=newx, deriv=0)

# solve for tangent at a given x
newx <- 0
pred0 <- predict(spl, x=newx, deriv=0)
pred1 <- predict(spl, x=newx, deriv=1)
yint <- pred0$y - (pred1$y*newx)
xint <- -yint/pred1$y


tang <- tibble(x = df$x) %>% 
  mutate(y = yint + pred1$y*x) %>% 
  filter(x > -2.0 & x < 2)

library(RColorBrewer)
colors <- brewer.pal(n = 4, name = "Dark2")
library(ggthemes)

ggplot() +
  geom_line(data = df, aes(x = x, y = y)) +
  geom_line(data = tang, aes(x= x, y = y)) +
  geom_vline(xintercept = 0) +
  ylim(-22,20) + 
  annotate(geom = "segment", x = 2, y = 10, xend = 2, yend = -20, color = colors[1]) +
  annotate(geom = "segment", x = 2, y = 10, xend = 0, yend = 10, color = colors[1]) +
  annotate(geom = "text", x = 1.9, y = -22 , label = "hat(beta)", parse = TRUE,
           hjust = "left", color = colors[1]) +
  annotate(geom = "text", x = -.75, y = 11, label = "L[1]", parse = TRUE,
           hjust = "left", color = colors[1]) +
  annotate(geom = "segment", x = -.45, y = 11, xend = -.05, yend = 10, 
    arrow = arrow(length = unit(2, "mm")), color = colors[1]) +
  annotate(geom = "text", x = .6, y = 5 , label = "L[0]", parse = TRUE,
           hjust = "left") +
  annotate(geom = "segment", x = .5, y = 5, xend = 0.1, yend = 6, 
    arrow = arrow(length = unit(2, "mm"))) +
  theme_few() +
  ylab (expression(paste("L(" , beta, ")"))) + 
  theme(axis.title.x=element_blank(), 
        axis.text.y=element_blank(), 
        axis.ticks.y=element_blank(),
        axis.title.y = element_text(angle = 0, vjust = .5)) +
  scale_x_continuous(breaks = c(0), label = c(expression(paste( beta, "= 0")))) +
  ggtitle("Figure 3.5")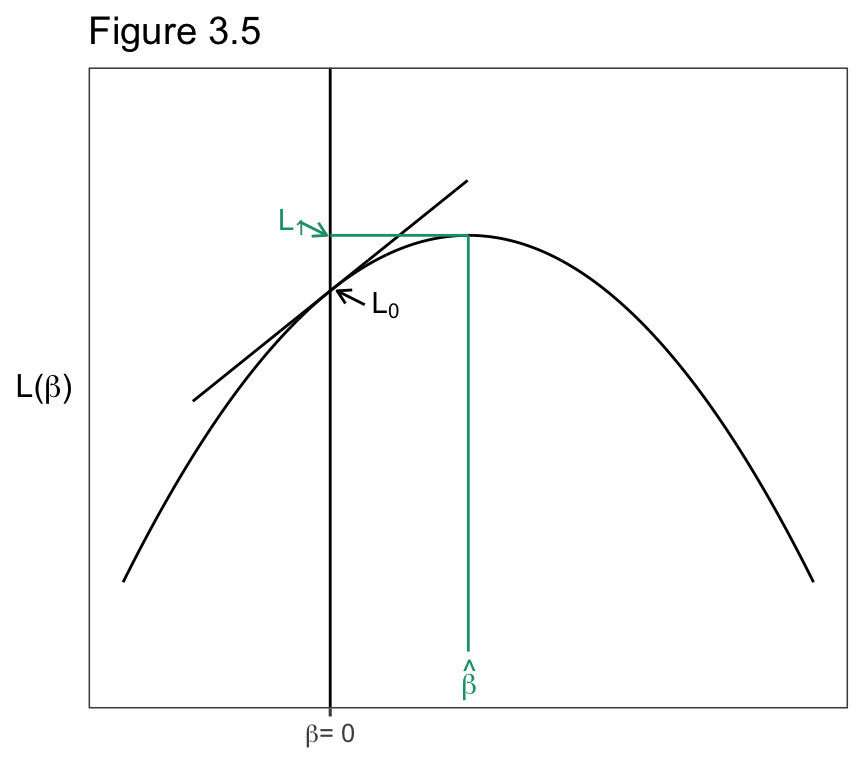

3.4.2 Example Political Ideology and Belief in Evolution

Evo <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Evolution.dat", 
                       header = TRUE, stringsAsFactors = FALSE)

n <- Evo$true + Evo$false

# gives a Wald z
fit <- glm(true/n ~ ideology, family = binomial, weights = n, data = Evo)

summary(fit)

Call:
glm(formula = true/n ~ ideology, family = binomial, data = Evo, 
    weights = n)

Deviance Residuals: 
      1        2        3        4        5        6        7  
 0.1430  -0.2697   1.4614  -1.0791   0.2922   0.4471   0.2035  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.75658    0.20500  -8.569   <2e-16 ***
ideology     0.49422    0.05092   9.706   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 113.20  on 6  degrees of freedom
Residual deviance:   3.72  on 5  degrees of freedom
AIC: 42.332

Number of Fisher Scoring iterations: 3
# Null deviance
pchisq(3.72, df=5, lower.tail=FALSE)
[1] 0.5903905
# Function to get the 95% Wald confidence interval.
waldCI <- function(x){
  list(lower = summary(x)$coefficients[, 1] + summary(x)$coefficients[, 2] *
         qnorm(.025,lower.tail=TRUE),
       upper = summary(x)$coefficients[, 1] + summary(x)$coefficients[, 2] *
         qnorm(.025,lower.tail=FALSE))
}

waldCI(fit)  # Wald CI
$lower
(Intercept)    ideology 
 -2.1583654   0.3944219 

$upper
(Intercept)    ideology 
 -1.3547930   0.5940161 
confint(fit)  # profile likelihood CI
Waiting for profiling to be done...
                2.5 %     97.5 %
(Intercept) -2.165294 -1.3609733
ideology     0.396166  0.5959414
library(car)  # for Anova function
Loading required package: carData

Attaching package: 'carData'
The following object is masked from 'package:vcdExtra':

    Burt
Anova(fit)  # likelihood-ratio tests for effect parameters in a GLM
Analysis of Deviance Table (Type II tests)

Response: true/n
         LR Chisq Df Pr(>Chisq)    
ideology   109.48  1  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
            # can also get with drop1(fit, test = "LRT")

library(statmod)  # for glm.scoretest
# null model
fit0 <- glm(true/n ~ 1, family = binomial, weights = n, data = Evo)  
glm.scoretest(fit0, Evo$ideology)^2  # score statistic with df = 1
[1] 104.101

\[\mathrm{Deviance}=2(L_S-L_M).\]

pchisq(113.20, df = 6, lower.tail=FALSE)  # model vs null (Null deviance)
[1] 4.353897e-22
pchisq(3.72, df=5, lower.tail=FALSE)  # model vs saturated (Residual deviance)
[1] 0.5903905

3.4.4 Model Comparison Using the Deviance

\[2(L_1-L_0)=2(L_S-L_0)-2(L_S-L1)= \mathrm{Deviance}_0 - \mathrm{Deviance}_1,\]

3.4.5 Residuals Comparing Ovservations to the Model Fit

\[\begin{equation} \mathrm{Pearson\ residual} = e_i =\frac{y_i-\hat\mu_i}{\sqrt{\widehat{var}(y_i)}} \tag{5} \end{equation}\]

\[\mathrm{Standardized\ residual} = e_i =\frac{y_i-\hat\mu_i}{SE}.\]

Evo %>% 
  bind_cols(`# sample` = .$true/n,  # .$ needed to use existing column
            `fitted` = fitted(fit),
            `std. res.` = rstandard(fit, type = "pearson"))
  ideology true false  # sample    fitted  std. res.
1        1   11    37 0.2291667 0.2205679  0.1611162
2        2   46   104 0.3066667 0.3168813 -0.3515386
3        3   70    72 0.4929577 0.4319445  1.6480176
4        4  241   214 0.5296703 0.5548525 -1.4995488
5        5   78    36 0.6842105 0.6713982  0.3248519
6        6   89    24 0.7876106 0.7700750  0.5413625
7        7   36     6 0.8571429 0.8459201  0.2206605

3.5 Fitting Generalized Linear Models

3.5.1 The Fisher Scoring Algorithm Fits GLMs

3.5.2 Bayesian Methods for Generalized Lineare Models

3.5.3 GLMs: A Unified Approach to Statistical Analysis

Random Component Link Function Explanatory Variables Model Chapter
Normal Identity Continuous Regression
Normal Identity Categorical Analysis of variance
Normal Identity Mixed Analysis of covariance
Binomial Logit Mixed Logistic regression 4-5, 8-10
Multinomial Logit Mixed Multinomial logit 8, 8-10
Poison Log Mixed Loglinear 7