6 Multicategory Logit Models

6.1 Baseline-Category Logit Models for Nominal Responses

6.1.1 Baseline-Category Logits

\[\mathrm{log}\left(\frac{\pi_j}{\pi_c}\right),\ j = 1, \dots,\ c-1.\]

\[\begin{equation} \mathrm{log}(\frac{\pi_j}{\pi_c}) = \alpha_j + \beta_j x,\ j = 1, \dots, c-1 \tag{10} \end{equation}\]

\[\begin{equation} \mathrm{log}(\frac{\pi_1}{\pi_2}) = \mathrm{log}\left(\frac{\pi_1/\pi_3}{\pi_2/\pi_3}\right) = \mathrm{log}\left(\pi_1/\pi_3\right) - \mathrm{log}\left(\pi_2/\pi_3\right) \\ = (\alpha_1 + \beta_1 x) - (\alpha_2 + \beta_2 x) \\ = (\alpha_1 -\alpha_2) + (\beta_1 - \beta_2) x \tag{11} \end{equation}\]

\[\begin{equation} \mathrm{log}(\frac{\pi_j}{\pi_c}) = \alpha_j + \beta_{j1} x_1 + \beta_{j2} x_2 + \dots + \beta_{jp} x_p \ j = 1, \dots, c-1 \tag{12} \end{equation}\]

6.1.2 Example: What Do Alligators Eat?

library(tidyverse)
Gators <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Alligators.dat",
                        header = TRUE, stringsAsFactors = TRUE)

Gators %>% 
  filter(row_number() %in% c(1, 2, n())) 
     x y
1 1.24 I
2 1.30 I
3 3.89 F
library(VGAM)  # package for multivariate GLMs, such s multinomial models 
Loading required package: stats4
fit <- vglm(y ~ x, family = multinomial, data = Gators)  # vglm = vector GLM
summary(fit)

Call:
vglm(formula = y ~ x, family = multinomial, data = Gators)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)   
(Intercept):1   1.6177     1.3073   1.237  0.21591   
(Intercept):2   5.6974     1.7937   3.176  0.00149 **
x:1            -0.1101     0.5171  -0.213  0.83137   
x:2            -2.4654     0.8996      NA       NA   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: log(mu[,1]/mu[,3]), log(mu[,2]/mu[,3])

Residual deviance: 98.3412 on 114 degrees of freedom

Log-likelihood: -49.1706 on 114 degrees of freedom

Number of Fisher scoring iterations: 5 

Warning: Hauck-Donner effect detected in the following estimate(s):
'x:2'


Reference group is level  3  of the response

\[\mathrm{log}(\hat\pi_1/\hat\pi_3) = 1.618 - 0.110x, \\ \mathrm{log}(\hat\pi_1/\hat\pi_2) = 5.697 - 2.465x. \]

\[\mathrm{log}(\hat\pi_1 / \hat\pi_2) = (1.618 - 5.697) + [- 0.110 - (- 2.465)]x = -4.080 + 2.355x.\]

fit2 <- vglm(y ~ x, family = multinomial(refLevel = 2), data = Gators) 
summary(fit2)

Call:
vglm(formula = y ~ x, family = multinomial(refLevel = 2), data = Gators)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)   
(Intercept):1  -4.0797     1.4686  -2.778  0.00547 **
(Intercept):2  -5.6974     1.7937  -3.176  0.00149 **
x:1             2.3553     0.8032      NA       NA   
x:2             2.4654     0.8996   2.741  0.00613 **
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: log(mu[,1]/mu[,2]), log(mu[,3]/mu[,2])

Residual deviance: 98.3412 on 114 degrees of freedom

Log-likelihood: -49.1706 on 114 degrees of freedom

Number of Fisher scoring iterations: 5 

Warning: Hauck-Donner effect detected in the following estimate(s):
'x:1'


Reference group is level  2  of the response
confint(fit2, method = "profile")
                   2.5 %    97.5 %
(Intercept):1 -7.3475058 -1.518699
(Intercept):2 -9.5913317 -2.485991
x:1            1.0111800  4.199073
x:2            0.8775186  4.463608
fit0 <- vglm(y ~ 1, family=multinomial, data = Gators)  # null model
deviance(fit0)  # deviance for working model is 98.3412
[1] 115.1419
VGAM::lrtest(fit, fit0)  # rltest function available in VGAM package for LR tests
Likelihood ratio test

Model 1: y ~ x
Model 2: y ~ 1
  #Df  LogLik Df  Chisq Pr(>Chisq)    
1 114 -49.171                         
2 116 -57.571  2 16.801  0.0002248 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# .00022 deviance diff = 2(log-like. diff.)

6.1.3 Estimating Response Probabilities

The response probabilities relate to the model parameters by \[\pi_j = \frac{e^{\alpha_j + \beta_{j1} x_1 + \beta_{j2} x_2 + \dots + \beta_{jp} x_p}} {\sum_{h=1}^c e^{\alpha_h + \beta_{h1} x_1 + \beta_{h2} x_2 + \dots + \beta_{hp} x_p}},\ j = 1, \dots , c.\]

fitted(fit) %>% 
  data.frame(.) %>% 
  filter(row_number() %in% c(1, 2, n())) 
           F           I          O
1  0.2265307 0.721964000 0.05150528
2  0.2502564 0.692466814 0.05727683
59 0.7630060 0.004733748 0.23226027
# obs 59 is alligator of length 3.89 meters
library(ggthemes)

library(RColorBrewer)
colors <- brewer.pal(n = 4, name = "Dark2")

fitted(fit) %>% 
  data.frame(.) %>% 
  bind_cols(length = Gators$x) %>% 
  rename("Fish" = F, "Invertebrates" = I, "Other" = O) %>% 
  pivot_longer(cols = c(Fish, Invertebrates, Other))  %>% 
  ggplot() + 
  geom_line(aes(x = length, y = value, color = name)) +
  scale_colour_manual(values=colors)+
  ylim(0, 1) + 
  xlim(1, 4) +
  xlab("Length of Alligator") +
  ylab("Predicted Probability") +
  theme_few() +
  annotate(geom = "segment", x = 2.8, y = 0.65, xend = 2.60, yend = .71, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[1]) +
  annotate(geom = "text", x = 2.825, y = 0.65, label = "Fish", 
           hjust = "left", color = colors[1]) +
  
  annotate(geom = "segment", x = 2.1, y = 0.45, xend = 1.80, yend = .42, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[2]) +
  annotate(geom = "text", x = 2.125, y = 0.45, label = "Invertebrates", 
           hjust = "left", color = colors[2]) + 
  
    annotate(geom = "segment", x = 2.1, y = 0.05, xend = 1.80, yend = .1, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[3]) +
  annotate(geom = "text", x = 2.125, y = 0.05, label = "Other", 
           hjust = "left", color = colors[3]) +
  theme(legend.position="none") +
  ggtitle("Figure 6.1")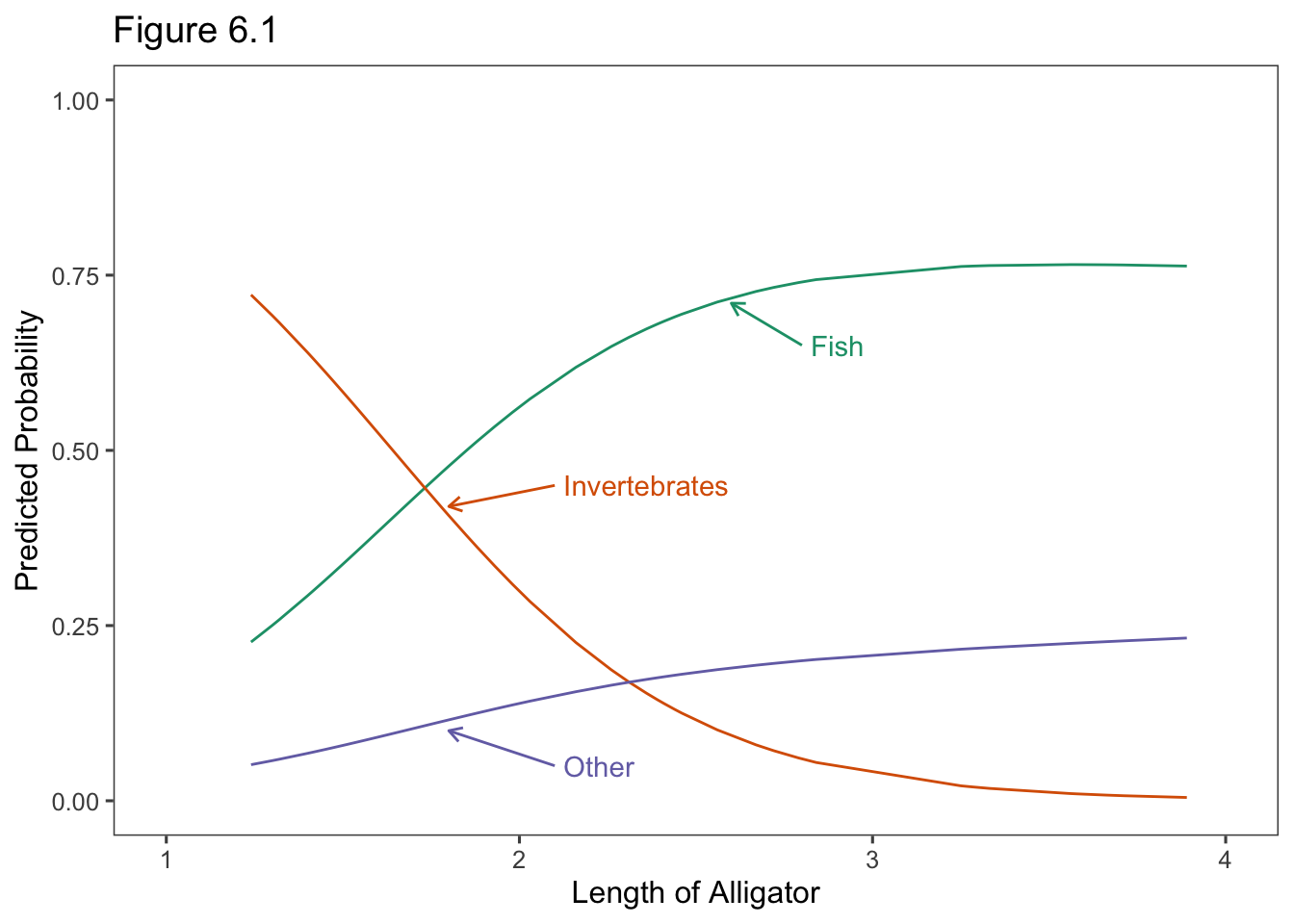

6.1.4 Checking multinomial Model Goodness of Fit

\[G^2 = 2\sum \mathrm{observed[log(observed/fitted)]}.\]

6.1.5 Example: Belief in Afterlife

Afterlife <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Afterlife.dat",
                        header = TRUE, stringsAsFactors = TRUE)
Afterlife
   race gender yes undecided no
1 white female 371        49 74
2 white   male 250        45 71
3 black female  64         9 15
4 black   male  25         5 13
library(VGAM)
fit <- vglm(cbind(yes, undecided, no) ~ gender + race, family = multinomial,
            data = Afterlife)

summary(fit)

Call:
vglm(formula = cbind(yes, undecided, no) ~ gender + race, family = multinomial, 
    data = Afterlife)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)    
(Intercept):1   1.3016     0.2265   5.747  9.1e-09 ***
(Intercept):2  -0.6529     0.3405  -1.918   0.0551 .  
gendermale:1   -0.4186     0.1713  -2.444   0.0145 *  
gendermale:2   -0.1051     0.2465  -0.426   0.6700    
racewhite:1     0.3418     0.2370   1.442   0.1493    
racewhite:2     0.2710     0.3541   0.765   0.4442    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: log(mu[,1]/mu[,3]), log(mu[,2]/mu[,3])

Residual deviance: 0.8539 on 2 degrees of freedom

Log-likelihood: -19.7324 on 2 degrees of freedom

Number of Fisher scoring iterations: 3 

No Hauck-Donner effect found in any of the estimates


Reference group is level  3  of the response
fit.gender <- vglm(cbind(yes, undecided, no) ~ gender, family = multinomial,
            data = Afterlife)

deviance(fit.gender)
[1] 2.848098
VGAM::lrtest(fit, fit.gender) # deviance dif = 2(log-likelihood. diff.)
Likelihood ratio test

Model 1: cbind(yes, undecided, no) ~ gender + race
Model 2: cbind(yes, undecided, no) ~ gender
  #Df  LogLik Df  Chisq Pr(>Chisq)
1   2 -19.732                     
2   4 -20.730  2 1.9942     0.3689
fit.race <- vglm(cbind(yes, undecided, no) ~ race, family = multinomial,
            data = Afterlife)

deviance(fit.race)
[1] 8.046504
VGAM::lrtest(fit, fit.race) # deviance dif = 2(log-likelihood. diff.)
Likelihood ratio test

Model 1: cbind(yes, undecided, no) ~ gender + race
Model 2: cbind(yes, undecided, no) ~ race
  #Df  LogLik Df  Chisq Pr(>Chisq)  
1   2 -19.732                       
2   4 -23.329  2 7.1926    0.02742 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
data.frame(Afterlife$race, Afterlife$gender, round(fitted(fit), 4))
  Afterlife.race Afterlife.gender    yes undecided     no
1          white           female 0.7546    0.0996 0.1459
2          white             male 0.6783    0.1224 0.1993
3          black           female 0.7074    0.1002 0.1925
4          black             male 0.6222    0.1206 0.2573

6.1.6 Discrete Choice Models*

6.1.7 Example: Shopping Destination Choice*

6.2 Cumulative Logit Models for Ordinal Responses {x6.2}

6.2.1 Cumulative Logit Models with Proportional Odds

\[\begin{equation} \mathrm{logit}[P(Y \le j)] = \alpha_j + \beta x,\ j = 1, \dots,\ c-1 \tag{13} \end{equation}\]

# https://rpubs.com/riazakhan94/logstcdistbasics
cdf=function(x,mu,s){
  k=(x-mu)/s
  return(1/(1+exp(-k)))
}

theData <- tibble(x=seq(-10,12,0.01)) %>% 
  mutate(curve0 = cdf(x, 0, 1)) %>% 
  mutate(curve2 = cdf(x, 2, 1)) %>% 
  mutate(curve4 = cdf(x, 4, 1))
  
library(ggthemes)  # theme_few 
theData %>% 
  ggplot(aes(x = x)) +
  geom_line(aes(y = curve0), color = colors[3]) +
  geom_line(aes(y = curve2), color = colors[2]) +
  geom_line(aes(y = curve4), color = colors[1]) +
  ggtitle("Figure 6.2") + 
  ylab(expression("P(Y" <= "j)")) +
  scale_y_continuous(breaks=c(0,1),
        labels=c("0", "1")) +
  theme_few() +
  theme(axis.text.x = element_blank(),
        axis.ticks.x = element_blank(),
        axis.title.y = element_text(angle = 0, vjust = 0.5),
        plot.title = element_text(hjust = 0.5)) +
    annotate(geom = "segment", x =-5, y = 0.55, xend = 0.0, yend = .55, 
           arrow = arrow(length = unit(2, "mm")), color = colors[3]) +
    annotate(geom = "text", x = -8, y = 0.55, label = paste("P(Y <= 3)"), 
             parse =  TRUE,hjust = "left", color = colors[3])  +

    annotate(geom = "segment", x =5, y = 0.65, xend = 2.75, yend = .65, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[2]) +
    annotate(geom = "text", x = 5, y = 0.65, label = paste("P(Y <= 2)"), 
             parse = TRUE, hjust = "left", color = colors[2]) +

    annotate(geom = "segment", x =7.5, y = 0.75, xend = 5.25, yend = .75, 
           arrow = arrow(length = unit(2, "mm")) , color = colors[1]) +
    annotate(geom = "text", x = 7.5, y = 0.75,  label = paste("P(Y <= 1)"), 
             parse = TRUE, hjust = "left", color = colors[1])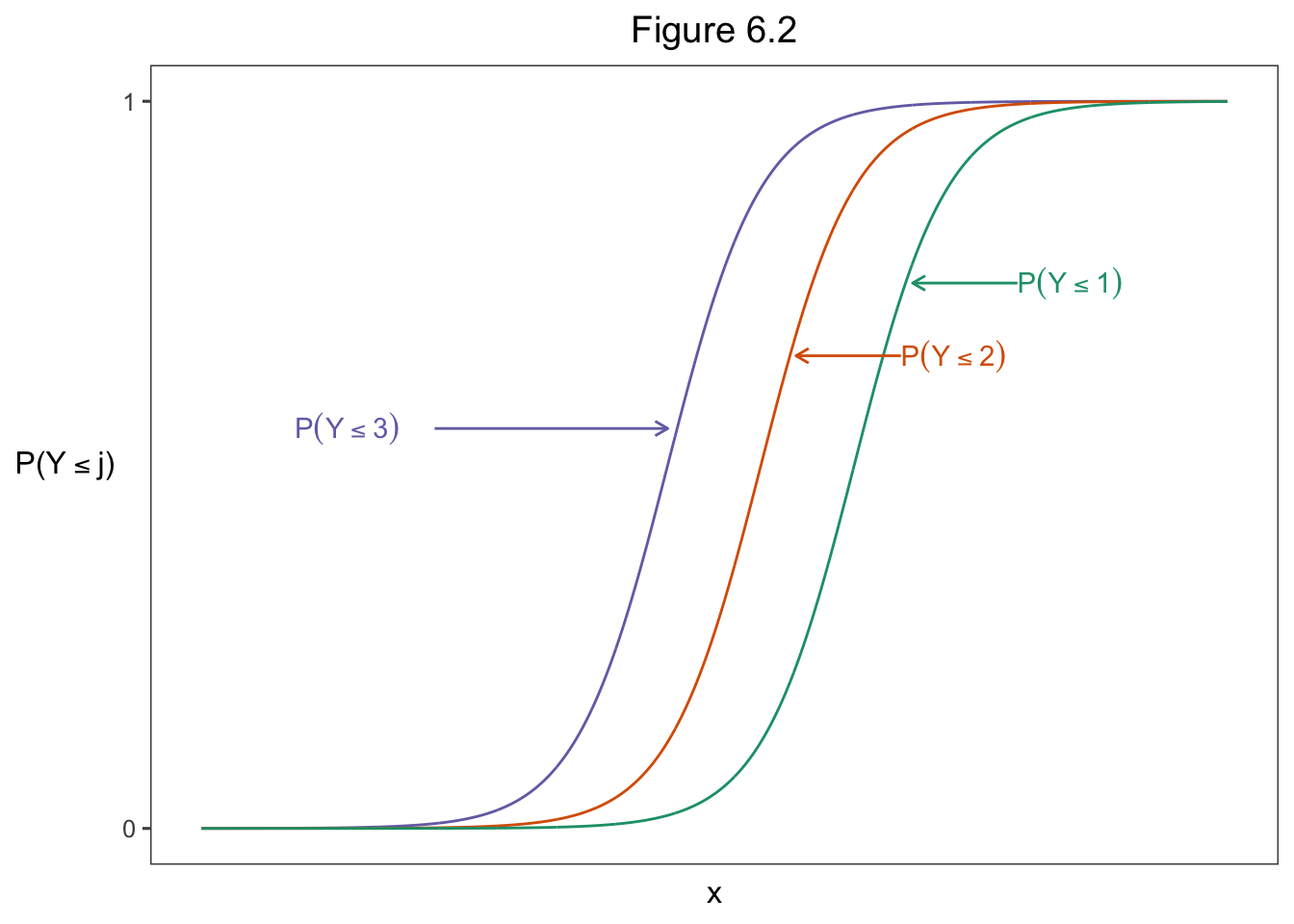

\[\frac{P(Y \le j\ |\ x = a) / P(Y > j\ |\ x = a)}{P(Y \le j\ |\ x = b) / P(Y > j\ |\ x = b)}.\]

\[\begin{equation} \mathrm{logit}[P(Y \le j)] = \alpha_j + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p,\ j = 1, \dots,\ c-1 \tag{14} \end{equation}\]

6.2.2 Example: Political Ideology and Political Party Affiliation

Polviews <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Polviews.dat",
                        header = TRUE, stringsAsFactors = TRUE)

Polviews
  gender party y1  y2 y3 y4 y5
1 female   dem 25 105 86 28  4
2 female repub  0   5 15 83 32
3   male   dem 20  73 43 20  3
4   male repub  0   1 14 72 32
library(VGAM)
# parallel = TRUE imposes proportional odds structure
# 4 intercepts for 5 y categories 
fit <-  vglm(cbind(y1,y2,y3,y4,y5) ~ party + gender, 
             family = cumulative(parallel = TRUE),
             data = Polviews)
summary(fit)  # same effects for all 4 logits

Call:
vglm(formula = cbind(y1, y2, y3, y4, y5) ~ party + gender, family = cumulative(parallel = TRUE), 
    data = Polviews)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)    
(Intercept):1 -2.12233    0.16875 -12.577   <2e-16 ***
(Intercept):2  0.16892    0.11481   1.471    0.141    
(Intercept):3  1.85716    0.15103  12.297   <2e-16 ***
(Intercept):4  4.65005    0.23496  19.791   <2e-16 ***
partyrepub    -3.63366    0.21785 -16.680   <2e-16 ***
gendermale     0.04731    0.14955   0.316    0.752    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: logitlink(P[Y<=1]), logitlink(P[Y<=2]), 
logitlink(P[Y<=3]), logitlink(P[Y<=4])

Residual deviance: 9.8072 on 10 degrees of freedom

Log-likelihood: -35.2032 on 10 degrees of freedom

Number of Fisher scoring iterations: 4 

No Hauck-Donner effect found in any of the estimates


Exponentiated coefficients:
partyrepub gendermale 
0.02641936 1.04844945

\[P(Y \le j) = \frac{\mathrm{exp}(\alpha_j + \beta_1 x_1 + \beta_2 x_2)}{1 + \mathrm{exp}(\alpha_j + \beta_1 x_1 + \beta_2 x_2)}.\]

\[P(Y=3)= P(Y \le 3) - P(Y \le 2).\]

Polviews <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Polviews.dat",
                        header = TRUE, stringsAsFactors = TRUE)

# y1 = very lib, y5 = very conservative.
data.frame(Polviews$gender, Polviews$party, round(fitted(fit), 4))
  Polviews.gender Polviews.party     y1     y2     y3     y4     y5
1          female            dem 0.1069 0.4352 0.3228 0.1256 0.0095
2          female          repub 0.0032 0.0272 0.1144 0.5895 0.2657
3            male            dem 0.1115 0.4423 0.3165 0.1206 0.0090
4            male          repub 0.0033 0.0284 0.1189 0.5927 0.2566

6.2.3 Inference about Cumulative Logit Model Parameters

fit2 <-  vglm(cbind(y1,y2,y3,y4,y5) ~ gender, 
             family = cumulative(parallel = TRUE),
             data = Polviews)
VGAM::lrtest(fit, fit2)
Likelihood ratio test

Model 1: cbind(y1, y2, y3, y4, y5) ~ party + gender
Model 2: cbind(y1, y2, y3, y4, y5) ~ gender
  #Df   LogLik Df  Chisq Pr(>Chisq)    
1  10  -35.203                         
2  11 -236.827  1 403.25  < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
fit <-  vglm(cbind(y1,y2,y3,y4,y5) ~ party + gender, 
             family = cumulative(parallel = TRUE),
             data = Polviews)

# profile likelihood CIs for beta_1 and beta_2 in full model
confint(fit, method = "profile")  
                    2.5 %     97.5 %
(Intercept):1 -2.46596771 -1.8014863
(Intercept):2 -0.05464962  0.3937706
(Intercept):3  1.56835767  2.1616181
(Intercept):4  4.20347943  5.1226824
partyrepub    -4.07163810 -3.2178566
gendermale    -0.24638939  0.3414038
fit <-  vglm(cbind(y5,y4,y3,y2,y1) ~ party + gender, 
             family = cumulative(parallel = TRUE),
             data = Polviews)

library(tidyverse)
confint(fit, method = "profile")  %>% 
  data.frame() %>% 
  rename(LCL= X2.5..) %>% 
  rename(UCL= X97.5..) %>% 
  rownames_to_column(var = "Param") %>% 
  filter(Param == "partyrepub") %>% 
  mutate(`LCL OR` = exp(LCL)) %>% 
  mutate(`UCL OR` = exp(UCL)) %>% 
  mutate(across(c("LCL", "UCL"), round, 3)) %>% 
  mutate(across(c("LCL OR", "UCL OR"), round, 1))
Warning: There was 1 warning in `mutate()`.
ℹ In argument: `across(c("LCL", "UCL"), round, 3)`.
Caused by warning:
! The `...` argument of `across()` is deprecated as of dplyr 1.1.0.
Supply arguments directly to `.fns` through an anonymous function instead.

  # Previously
  across(a:b, mean, na.rm = TRUE)

  # Now
  across(a:b, \(x) mean(x, na.rm = TRUE))
       Param   LCL   UCL LCL OR UCL OR
1 partyrepub 3.218 4.072     25   58.7

6.2.4 Increased Power for Ordinal Analyses

6.2.5 Example: Happiness and Family Income

Happy <- read.table("http://users.stat.ufl.edu/~aa/cat/data/Happy.dat",
                    header = TRUE, stringsAsFactors = TRUE)

Happy
  income y1 y2 y3
1      1 37 90 45
2      2 25 93 56
3      3  6 18 13
fit <- vglm(cbind(y1, y2, y3) ~ income, family = cumulative(parallel = TRUE),
            data = Happy)
fit0 <- vglm(cbind(y1, y2, y3) ~ 1, family = cumulative(parallel = TRUE),
            data = Happy)
VGAM::lrtest(fit, fit0)
Likelihood ratio test

Model 1: cbind(y1, y2, y3) ~ income
Model 2: cbind(y1, y2, y3) ~ 1
  #Df  LogLik Df Chisq Pr(>Chisq)  
1   3 -14.566                      
2   4 -16.121  1 3.109    0.07786 .
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
fit2 <- vglm(cbind(y1, y2, y3) ~ factor(income), family = multinomial,
            data = Happy)
fit0 <- vglm(cbind(y1, y2, y3) ~ 1, family = multinomial,
            data = Happy)
Warning in vglm.fitter(x = x, y = y, w = w, offset = offset, Xm2 = Xm2, : some
quantities such as z, residuals, SEs may be inaccurate due to convergence at a
half-step
# baseline cat logit null model equivalent to cumulative logit null model
VGAM::lrtest(fit2, fit0)
Likelihood ratio test

Model 1: cbind(y1, y2, y3) ~ factor(income)
Model 2: cbind(y1, y2, y3) ~ 1
  #Df  LogLik Df  Chisq Pr(>Chisq)
1   0 -14.058                     
2   4 -16.121  4 4.1258     0.3892

6.2.6 Latent Variable Linear Models Imply Cumulative Link Models

\[y = j\ \mathrm{if}\ \alpha_{j-1} < y^* \le \alpha_j.\]

\[Y^* = \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_p x_p + \epsilon,\]

\[\begin{equation} \mathrm{link}[P(Y \le j)] = \alpha_j - \beta_1 x_1 - \beta_2 x_2 - \cdots - \beta_p x_p,\ j = 1, \dots,\ c-1 \tag{15} \end{equation}\]

6.2.7 Invariance to Choice of Response Categories

6.4 Paired-Category Logit Modeling of Ordinal Response *

6.4.1 Adjacent-Categories Logits

\[\mathrm{log}\left(\frac{\pi_j}{\pi_{j+1}}\right),\ j = 1, \dots, c-1.\] \[\begin{equation} \mathrm{log}\left(\frac{\pi_j}{\pi_{j+1}}\right) = \alpha_j + \beta x,\ j = 1, \dots, c-1. \tag{16} \end{equation}\]

6.4.2 Example: Political Ideology Revisited

fit <- vglm(cbind(y1,y2,y3,y4,y5) ~ party + gender, 
           family = acat(parallel = TRUE, reverse = TRUE), 
           data = Polviews)
# family=acat gives adjacent-category logits
summary(fit)

Call:
vglm(formula = cbind(y1, y2, y3, y4, y5) ~ party + gender, family = acat(parallel = TRUE, 
    reverse = TRUE), data = Polviews)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)    
(Intercept):1 -1.38707    0.17079  -8.121 4.61e-16 ***
(Intercept):2  0.36218    0.11749   3.083  0.00205 ** 
(Intercept):3  0.77529    0.14720   5.267 1.39e-07 ***
(Intercept):4  2.99240    0.23132  12.936  < 2e-16 ***
partyrepub    -2.23478    0.16841 -13.270  < 2e-16 ***
gendermale     0.01212    0.09661   0.125  0.90016    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: loglink(P[Y=1]/P[Y=2]), loglink(P[Y=2]/P[Y=3]), 
loglink(P[Y=3]/P[Y=4]), loglink(P[Y=4]/P[Y=5])

Residual deviance: 13.4665 on 10 degrees of freedom

Log-likelihood: -37.0329 on 10 degrees of freedom

Number of Fisher scoring iterations: 4 

Warning: Hauck-Donner effect detected in the following estimate(s):
'partyrepub'
pValue <- 1 - pchisq(13.47, 10)
format(round(pValue, 8), scientific = FALSE)
[1] "0.1985672"

6.4.3 Sequential Logits

6.4.4 Example: Tonsil Size and Streptococcus

Tonsils <- tibble(carrier = c("yes", "no"), y1 = c(19, 497), 
                  y2 = c(29, 560), y3 = c(24, 269))

fit <- vglm(cbind(y1, y2, y3) ~ carrier, family = sratio(parallel = TRUE),
            data = Tonsils)
summary(fit)

Call:
vglm(formula = cbind(y1, y2, y3) ~ carrier, family = sratio(parallel = TRUE), 
    data = Tonsils)

Coefficients: 
              Estimate Std. Error z value Pr(>|z|)    
(Intercept):1 -0.51102    0.05614  -9.102  < 2e-16 ***
(Intercept):2  0.73218    0.07286  10.049  < 2e-16 ***
carrieryes    -0.52846    0.19775  -2.672  0.00753 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Names of linear predictors: logitlink(P[Y=1|Y>=1]), logitlink(P[Y=2|Y>=2])

Residual deviance: 0.0057 on 1 degrees of freedom

Log-likelihood: -11.7659 on 1 degrees of freedom

Number of Fisher scoring iterations: 3 

No Hauck-Donner effect found in any of the estimates